Teoria dos conjuntos

   Teoria dos conjuntos

  1. Conjuntos: É um conceito primitivo da matemática, que não cabe definição, mas, podemos dizer que conjunto é uma reunião, coleção ou agrupamento de elementos. Estes podem ser descritos de diferentes maneiras, a mais visual é por listagem A={2,3,5,7,11,13,...}, mas, podemos representar da seguinte forma, A={x/x é um número primo}.

  2. Conjunto vazio: Dizemos que um conjunto que não possui elementos, é um conjunto vazio, e podemos representá-lo da seguinte maneira: { } ou 0, mas nunca {0}, o que seria um erro.

  3. Relação de pertinência: Utilizamos esta relação, na tratativa de elementos para conjuntos, assim, quando queremos dizemos que um elemento pertence a um determinado conjunto, estamos utilizando esta relação.

   4. Subconjuntos: Quando todo elemento de um conjunto A, também pertencer a um conjunto B, podemos inferir que, A é subconjunto de B. Logo, dizemos que todo A é subconjunto de A. Existe uma relação de potenciação presente nesta relação, é que para descobrir a quantidade de elementos de um conjunto, basta que calculemos dois elevado a n, onde n é o número de elementos do nosso conjunto. Se A={1,2,3,4,5}, então dizemos que A possui subconjuntos. 

   5. Conjuntos numéricos: São ditos conjuntos numéricos, todos os conjuntos, cujos elementos são números.
   5.1. Naturais:Pertencem ao conjunto dos naturais os números inteiros positivos, incluindo o zero. Esse conjunto é representado pela letra N maiúscula. Os elementos dos conjuntos devem estar sempre entre chaves. Lembrando que nem todas as operações aritméticas básicas que conhecemos, acontecem neste conjunto.
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ... } 

   5.2. Inteiros: Pertencem ao conjunto dos números inteiros, os números negativos e também o Conjunto dos Números Naturais. 
Os números positivos são opostos aos números negativos e os negativos opostos aos positivos. 
Sua representação é feita pela letra Z maiúscula. A cada número natural k, podemos associar um número -k, denominado simétrico ou oposto. 

Z = {..., -4, -3, -2, -1, 0, +1, +2, +3,...} 

   5.3. Racionais:O conjunto dos números racionais engloba todos os algarismos na forma de a/b, com b ≠ 0, isto é, os números fracionários e as dízimas periódicas (números decimais). O conjunto é representado pela letra Q maiúscula.

    

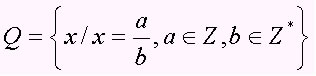
   5.4. Irracionais: Os números irracionais são aqueles que não podem ser representados por meio de uma fração. O surgimento desses números veio de um antigo problema que Pitágoras se recusava a aceitar, que era o cálculo da diagonal de um quadrado, cujo lado mede 1 unidade, diagonal esta que mede √2. Este número deu início ao estudo de um novo conjunto, representado pelos números irracionais. Exemplo:
3, 254127896542...

0, 32478139852...

2, 365874412...

O valor de π é um número irracional π = 3, 1415...

    5.5 Reais: O conjunto dos números reais surge para designar a união do conjunto dos números racionais e o conjunto dos números irracionais. É importante lembrar que o conjunto dos números racionais é formado pelos seguintes conjuntos: Números Naturais e Números Inteiros. Vamos exemplificar os conjuntos que unidos formam os números reais. 

         
   6. Reta real: Ao conjunto dos números reais, podemos associar o conjunto dos infinitos pontos de uma reta, onde definimos:
   O ponto O, e dizemos origem;
   Um sentido positivo e um sentido negativo.

            

   6.1. Igualda e desigualdade: Dados dois números reais a e b, ocorre uma e somente uma, das seguintes relações:
   a=b   ou a < b   ou a > b.

     7. Intervalos reais: Alguns subconjuntos contínuos, são denominados de intervalos reais, geralmente definidos por desigualdades, caracterizados pelas inequações.
   Intuitivamente, um intervalo real é um subconjunto dos números reais que não tem nenhum buraco. Ou seja, se I é um intervalo, a e b são elementos deste intervalo com a < b, então todo número entre a e b também pertence ao intervalo.
Os intervalos são classificados de acordo com seus extremos (o extremo superior e o extremo inferior). Cada extremo pode ser ilimitados, limitado e aberto ou limitado e fechado.
Representa-se o intervalo através do seu limite inferior, seguido da vírgula (ou ponto-e-vírgula) e o limite superior.
Costuma-se representar o limite inferior por:

•  - ilimitado
•  - limitado e aberto
•  - limitado e fechado

Sendo o limite superior representado por:

•  - ilimitado
•  - limitado e aberto
•  - limitado e fechado

Por exemplo:

•  - é o conjunto dos números reais não-positivos
•  - é o conjuntos dos números reais x em que x ≥ 1 e x < .

      Intervalo aberto em a e aberto em b, ]a,b[ , {xЄR/a < x < b}

Aberto à esquerda e aberto à direita




Intervalo aberto em a e fechado em b, ]a,b], {xЄR/a < x ≤ b}
Aberto à esquerda e fechado à direita




Intervalo fechado em a e aberto em b, [a,b[, {xЄR/a ≤ x < b}
Fechado à esquerda e aberto à direita



Intervalo fechado em a e fechado em b, [a,b], {xЄR/a ≤ x ≤ b}
Fechado à esquerda e fechado à direita

Intervalos infinitos

{xЄR/x > a}

{xЄR/x<a}


{xЄR/x≥a}



{xЄR/≤a}